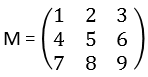
comforttore.blogg.se - Eigenvectors mathematica

#Eigenvectors mathematica how to
#Eigenvectors mathematica free

Ax = b has a unique solution for each b in R n.

The columns of A are linearly independent.

Let A be an n × n matrix, and let T : R n → R n be the matrix transformation T ( x )= Ax. We now have two new ways of saying that a matrix is invertible, so we add them to the invertible matrix theorem. Subsection 5.1.3 The Invertible Matrix Theorem: Addenda These are exactly the nonzero vectors in the null space of A. Ĭoncretely, an eigenvector with eigenvalue 0 is a nonzero vector v such that Av = 0 v, i.e., such that Av = 0. In this case, the 0-eigenspace is by definition Nul ( A − 0 I n )= Nul ( A ). We know that 0 is an eigenvalue of A if and only if Nul ( A − 0 I n )= Nul ( A ) is nonzero, which is equivalent to the noninvertibility of A by the invertible matrix theorem in Section 3.6.

In this case, the 0-eigenspace of A is Nul ( A ).

The number 0 is an eigenvalue of A if and only if A is not invertible.We conclude with an observation about the 0-eigenspace of a matrix. The eigenvectors with eigenvalue λ are the nonzero vectors in Nul ( A − λ I n ), or equivalently, the nontrivial solutions of ( A − λ I n ) v = 0.

#Eigenvectors mathematica free

The dimension of the λ-eigenspace of A is equal to the number of free variables in the system of equations ( A − λ I n ) v = 0, which is the number of columns of A − λ I n without pivots.

In this case, finding a basis for the λ-eigenspace of A means finding a basis for Nul ( A − λ I n ), which can be done by finding the parametric vector form of the solutions of the homogeneous system of equations ( A − λ I n ) v = 0.

λ is an eigenvalue of A if and only if ( A − λ I n ) v = 0 has a nontrivial solution, if and only if Nul ( A − λ I n ) A =.

Let A be an n × n matrix and let λ be a number.

#Eigenvectors mathematica how to

We will learn how to do this in Section 5.2.Įxample (Reflection) Recipes: Eigenspaces On the other hand, given just the matrix A, it is not obvious at all how to find the eigenvectors. If someone hands you a matrix A and a vector v, it is easy to check if v is an eigenvector of A : simply multiply v by A and see if Av is a scalar multiple of v. We do not consider the zero vector to be an eigenvector: since A 0 = 0 = λ 0 for every scalar λ, the associated eigenvalue would be undefined. NoteĮigenvalues and eigenvectors are only for square matrices.Įigenvectors are by definition nonzero. On the other hand, “eigen” is often translated as “characteristic” we may think of an eigenvector as describing an intrinsic, or characteristic, property of A. An eigenvector of A is a vector that is taken to a multiple of itself by the matrix transformation T ( x )= Ax, which perhaps explains the terminology. The German prefix “eigen” roughly translates to “self” or “own”. If Av = λ v for v A = 0, we say that λ is the eigenvalue for v, and that v is an eigenvector for λ.

An eigenvalue of A is a scalar λ such that the equation Av = λ v has a nontrivial solution.

An eigenvector of A is a nonzero vector v in R n such that Av = λ v, for some scalar λ.

Here is the most important definition in this text.

Subsection 5.1.1 Eigenvalues and Eigenvectors As such, eigenvalues and eigenvectors tend to play a key role in the real-life applications of linear algebra.

These form the most important facet of the structure theory of square matrices. In this section, we define eigenvalues and eigenvectors. Essential vocabulary words: eigenvector, eigenvalue.Theorem: the expanded invertible matrix theorem.Pictures: whether or not a vector is an eigenvector, eigenvectors of standard matrix transformations.Recipe: find a basis for the λ-eigenspace.Learn to decide if a number is an eigenvalue of a matrix, and if so, how to find an associated eigenvector.Learn to find eigenvectors and eigenvalues geometrically.Learn the definition of eigenvector and eigenvalue.Section 5.1 Eigenvalues and Eigenvectors ¶ Objectives Hints and Solutions to Selected Exercises.3 Linear Transformations and Matrix Algebra